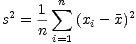
Calculating the best standard deviation estimate of a normally distributed process, for small N

Frank Palazzolo

January 25, 2006

Calculating the best standard deviation estimate for small N can be tricky. First of all, calculating the sample variance s² is reasonably straightforward

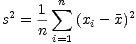
2 1 sum n 2 s = n (xi- x) i=1

But wait, have you seen this formula with n replaced by n- 1? Ever wonder why that is? To get the so-called ”unbiased” estimate for the variance, you must use the relation

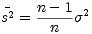
s2 = n--1s2 n

to estimate the original variance 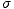²

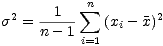
1 sum n s2 = ----- (xi- x)2 n - 1i=1

This is where the infamous n- 1 comes from. This is all well and good, but what about estimating the standard deviation? A sample standard deviation s can be defined by

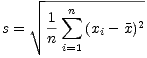
------------- sum n s = V~ 1 (xi- x)2 n i=1

Because of the non-linearity of the square root, the mean of this distribution is not simple. Unfortunately, is also dependant of the distribution of the original process. For normally distributed random variables, it has a mean of

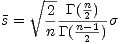
V~ -- n s = 2-G(-2)-s n G(n-21)

where 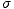is the actual standard deviation of the original process. To recover the best estimate of 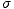for small n, we need to multiply our standard deviation by a compensation factor of

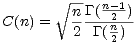
V~ -- n-1 C(n) = n-G(-2-)- 2 G(n2)

In general, C(n) is not easy to calculate in a general purpose computer language, unless you have access to the Gamma function. Even if you do, the Gamma function will overflow for moderately sized n, even while C(n) is bounded.

I found a really simple way to generate a table of these values in an iterative manner. The trick was to make use of the identity

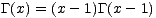
G(x) = (x -1)G(x - 1)

and calculate the relation

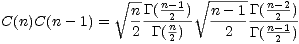
V~ -- V~ ----- n-G(n-21)- n---1G(n-22)- C(n)C(n - 1) = 2 G(n) 2 G(n-1) 2 2

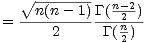
V~ -------- --n(n--1)G(n-22) = 2 G(n2)

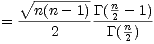
V~ -------- --n(n---1) G(n2--1)- = 2 G(n2)

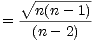
V~ -------- = --n(n--1) (n - 2)

and the 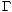’s are gone! We simply need to start with the initial value

V~ - C(2) = p

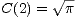
And built a table of C(n) based on the value of C(n - 1), for some reasonable range of 2 < n < n_max.

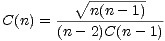
V~ n(n---1) C(n) = -------------- (n - 2)C(n - 1)

In my implementation, 32767 was plenty. The effect is only important for small n as lim_nC(n) = 1

Now, when we need to calculate a standard deviation based on n samples, we can use

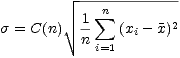
------------- sum n s = C(n) V~ 1- (xi- x)2 ni=1

And we will have the best possible estimate, if the original random variable is normal.